| Designation | Board Offset | Illustration | Corner Axis |
|---|---|---|---|
| upright | None |
|
(0,0,n) |
| cant | X=1 |
|
(n,0,n) |
| slant | Y=1 |
|
(0,n,n) |
| skew | X=1, Y=1 |
|
(n,n,n) |
|
Musings on 3D ChessTable of Contents
2.1. Arrangements |
A 2D board is laid out in files and ranks. Files are the X direction and ranks are the Y direction. This notion is supported by the standard algebraic notation. A 3D board adds levels, which correspond to the Z direction (and obeys the right-hand rule for people who think in vectors).
Premise 1: Chessboard notation is (file)(rank)(level), where files are lettered a, b, c, etc., ranks are numbered 1, 2, 3, etc., and levels are lettered A, B, C, etc.
Chessboard notation is an extension of the 2D game algebraic notation: files are a, b, c, etc. and ranks are 1, 2, 3, etc. Levels are designated A, B, C, etc.
The chessboard notation is formatted as follows :
(file)(rank)(level)
In all chessboard configurations, the left-most, white-side, bottom-level cell is designated a1A whether that cell is usable or not.
In designing a 3D chessboard, three features are important:
A usable cell is considered part of play and a legitimate destination for a piece move. Unusable cells may not be involved in play. Cells may remain usable or unusable for the entire game, or they may transition from usable to unusable depending on the rules of a particular variation.
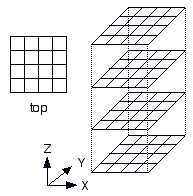
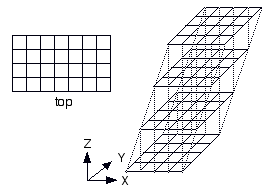
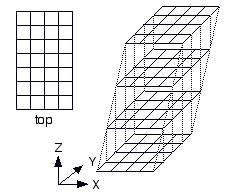
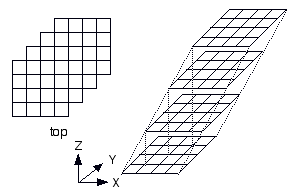
Notice this premise doesn't specify how the boards are arranged vertically. The boards could be aligned vertically, offset in the file (X) direction, offset in the rank (Y) direction, or offset in both the file (X) and rank (Y) directions. I will call these upright, cant, slant, and skew respectively.
Premise 3: 2D boards are offset 0 or 1 unit for each increase in level in either the X direction, the Y direction, or both the X and Y directions.
This premise establishes that the offset can be at most one per level
and increases linearly.
The
corner axis is the line which describes the up direction for
the chessboard. This vector becomes relevant when piece movement is
discussed.
| Designation | Board Offset | Illustration | Corner Axis |
|---|---|---|---|
| upright | None |

|
(0,0,n) |
| cant | X=1 |

|
(n,0,n) |
| slant | Y=1 |

|
(0,n,n) |
| skew | X=1, Y=1 |

|
(n,n,n) |
Example: The classic Tridimensional Chess variation uses a slant board.
Premise 5: Vertically, the chessboard
cell colors may be varying or constant.
This premise requires us to consider how the colored cells are arranged vertically. The cells can vary in color along the Z axis, or the cells can be constant in color. I will call these varying and constant respectively.
| Designation | Illustration | Designation | Illustration |
|---|---|---|---|
| varying |
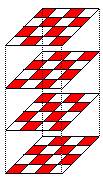
|
constant |
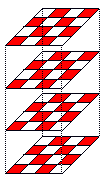
|
Example: The classic Tridimensional Chess variation uses constant markings.
Notice that a 4x4x4 upright chessboard consisting of 64 cells, when converted to a slant board transforms to dimensions of 4x7x4 with 64 usable cells out of 112 possible.
Example: The classic Tridimensional Chess variation uses a chessboard with dimensions 6x10x7, with 64 usable cells (some of which are movable!).
Example: A chessboard with characteristics (upright, varying, 4x4x4) is a classic rearrangement of the standard 64 squares into 3D. The chessboard contains 64 usable squares of 64 possible.
| Table of Contents | Previous: Introduction | Next: Piece Movement |